FISICA IV

5º. Semestre

UNIDAD I: ESTATICA

La mecánica es una rama de la Física, dedicada al estudio de los movimientos y estados en que se encuentran los cuerpos. Describe y predice las condiciones del reposo y movimiento de los cuerpos, bajo la acción de los cuerpos, bajo la acción de las fuerzas. Se divide en dos partes: Cinemática que estudia las diferentes clases de movimiento de los cuerpos sin atender las causas que lo producen y la dinámica que estudia las causas que originan el movimiento de los cuerpos. La estática queda comprendida dentro del estudio de la dinámica, analiza las causas que permiten el equilibrio de los cuerpos.

La palabra estática se deriva del griego estáticos que significa inmóvil. La estática, como parte de la dinámica, se encarga de estudiar todos aquellos casos en que los cuerpos sometidos a la acción de varias fuerzas no se mueven, toda vez que las fuerzas se equilibran entre si. También estudia aquellos casos en que la resultante de las fuerzas que actúan sobre un cuerpo en movimiento es nula y el cuerpo sigue desplazándose con movimiento rectilíneo uniforme.

1.1 VECTORES.

1.1.1 Introducción.

Algunas cantidades pueden describirse totalmente por un número y una unidad. Sólo importan las magnitudes en los casos de un área de 12 m², un volumen de 40 ft³, una distancia de 50 km. Este tipo de cantidades se llaman cantidades escalares.

Una cantidad escalar se especifica totalmente por su magnitud, que consta de un número y una unidad. Por ejemplo: rapidez (15 mi/hr), distancia (12 km) y volumen (200 cm³).

Algunas cantidades físicas, como la fuerza y la velocidad, tienen dirección, sentido y además magnitud. Por eso se les llama cantidades escalares.

Una cantidad vectorial se especifica totalmente por una magnitud, un sentido y una dirección. Por ejemplo desplazamiento (20 m, norte) y velocidad (40 mi/hr, 30° Norte).

Características de un vector

Un vector cualquiera tiene las siguientes características:

1. Punto de aplicación u origen.

2. Magnitud. Indica su valor y se representa por la longitud del vector de acuerdo a su escala convencional.

3. Dirección. Señala la línea sobre la cual actúa.

4. Sentido. Indica hacia donde va el vector.

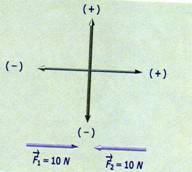
Fig. 1.1 Estos vectores tienen la misma dirección

pero diferente sentido.

Clasificación de los vectores.

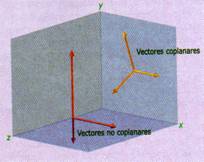Los vectores pueden clasificarse en coplanares, si se encuentran en el mismo plano, o en dos ejes, y no coplanares si están en diferente plano, es decir, en tres ejes.

Fig. 1.2 Ejemplos de vectores coplanares

y no coplanares.

Sistema de vectores.

Se tiene un sistema de vectores colineales cuando dos o más vectores se encuentran en la misma dirección o línea de acción. Un sistema de vectores es concurrente cuando la dirección o línea de acción de los vectores se cruza en algún punto.

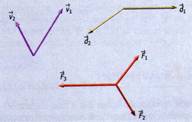
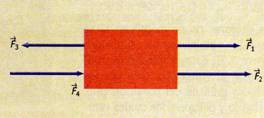
Fig. 1.3 Sistema de vectores colineales. Fig. 1.4 Ejemplos de vectores concurrentes.

Propiedades de los vectores.

Los vectores tienen las siguientes propiedades: propiedad de transmisibilidad del punto de aplicación, el efecto externo de un vector no se modifica si es trasladado en su misma dirección, es decir, sobre su propia línea de acción; propiedad de los vectores libres, los vectores no se modifican si se trasladan paralelamente a sí mismos.

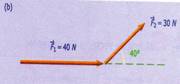
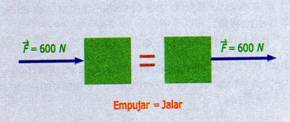Fig. 1.6 Propiedad de los vectores libres. (a) Dos vectores

Fig. 1.5 Propiedad de transmisibilidad del libres. (b) Los vectores no se modifican si se

punto de aplicación de un vector. trasladan paralelamente a sí mismos.

Resultante y equilibrante de un sistema de vectores.

La resultante de un sistema de vectores es el vector que produce él sólo, el mismo efecto que los demás vectores del sistema. Por ello un vector resultante es aquel capaz de sustituir un sistema de vectores.

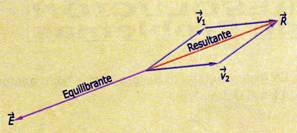La equilibrante de un sistema de vectores, como su nombre lo indica, es el vector encargado de equilibrar el sistema. Por tanto, tiene la misma magnitud y dirección que la resultante, pero con sentido contrario.

Fig. 1.7 Resultante y equilibrante de un sistema de vectores.

1.1.2 Suma de vectores. (Métodos gráficos)

Para sumar vectores se deben utilizar métodos diferentes a una simple suma aritmética. Estos métodos pueden ser gráficos o analíticos, pero en ambos casos se consideran además de la magnitud del vector, su dirección y sentido.

Método del polígono.

1. Elija una escala y determine la longitud de las flechas que corresponden a cada vector.

2. Dibuje a escala una flecha que represente la magnitud, sentido y dirección del primer vector.

3. Dibuje la flecha del segundo vector de modo que la cola coincida con la punta de la flecha del primer vector.

4. Continúe el proceso de unir el origen de cada vector con las puntas hasta que la magnitud y la dirección de todos los vectores queden bien representados.

5. Dibuje el vector resultante con el origen (punto de partida) y la punta de flecha unida a la punta del último vector.

6. Mida con regla y transportador para determinar la magnitud y dirección del vector resultante.

Ejemplo 1:

Un jinete y su caballo cabalgan 3 km al norte y después 4 km al oeste. Calcular:

a) ¿Cuál es la distancia total que recorren?

b) ¿Cuál fue su desplazamiento?

Solución:

a) Como la distancia es una magnitud escalar, encontramos la distancia total recorrida al sumar aritméticamente las dos distancias:

d_t = d₁ + d₂ = 3 km + 4 km = 7 km

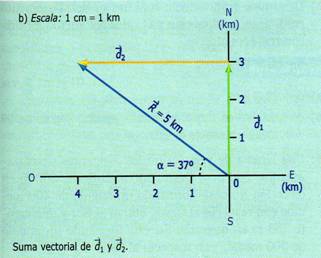
b) Para encontrar su desplazamiento, dibujamos a escala el primer desplazamiento de 3 km realizado al norte, representado por d₁ y después el segundo desplazamiento de 4 km al oeste representado por d₂. Posteriormente unimos el origen de d₁ con el extremo del vector d₂ a fin de encontrar el vector resultante R equivalente a la suma vectorial de los dos desplazamientos. El origen del vector resultante R es el mismo que tiene el vector d₁ y su extremo coincide con el del vector d₂. Para calcular la magnitud de R medimos su longitud de acuerdo con la escala utilizada y su dirección se determina por el ángulo α que forma. Así, encontramos que

R = 5 km con un ángulo α de 37 º en dirección noreste.

Ejemplo 2:

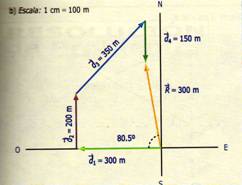
Una lancha de motor efectúa los siguientes desplazamientos: 300 m al Oeste, 200 m al Norte, 350 m al Noreste y 150 m al Sur. Calcular:

a) ¿Qué distancia total recorre?

b) Determinar gráficamente cuál es su desplazamiento resultante, en qué dirección actúa y cuál es el valor de su ángulo medido con respecto al Oeste.

Solución:

a) La distancia total es igual a: d_t = d₁ + d₂ + d₃ + d₄

d_t = 300 m + 200 m + 350 m + 150 m = 1000 m

b) Como se ve en la figura el desplazamiento total de la lancha es de 300 m en una dirección Noreste que forma un ángulo de 80.5º medido con respecto al Oeste.

Ejercicios en clase:

1.- Un barco recorre 100 km hacia el norte durante el primer día de viaje, 60 km al noreste el segundo día, y 120 km hacia el este el tercer día. Encuentre el desplazamiento resultante con el método del polígono.

2.- Una ardilla camina en busca de comida, efectuando los siguientes desplazamientos: 15 m al sur, 23 m al este, 40 m en dirección noreste con un ángulo de 35º medido despecto al este, 30 m en dirección noroeste que forma un ángulo de 60º medido respecto al oeste, y finalmente 15 m en una dirección sureste con un ángulo de 40º medido respecto al oeste. Calcular:

a) ¿Cuál es la distancia total recorrida?

b) Mediante una escala conveniente represente gráficamente los desplazamientos; determine el valor del desplazamiento resultante, la dirección en que se efectúa y el valor del ángulo formado respecto al este.

Ejercicios de tarea:

1.- Un jugador de fútbol americano efectúa los siguientes desplazamientos: 6 m al este, 4 m en dirección noreste y finalmente 2 m al norte. Calcular:

a) ¿Cuál es la distancia total que recorre?

b) Encuentre en forma gráfica cuál fue su desplazamiento resultante, en qué dirección actúa y cual es el valor del ángulo medido con respecto al este.

2.- Una lancha de vela realiza los siguientes desplazamientos: 300 m al oeste, 200m al norte, 350 m en dirección noroeste formando un ángulo de 40º medido con respecto al oeste, 600 m al sur y finalmente 250 m en dirección sureste formando un ángulo de 30º medido con respecto al este. Calcular:

a) ¿Cuál es la distancia total recorrida?

b) Determinar gráficamente el valor del desplazamiento resultante, la dirección en que se efectúa y el valor del ángulo formado respecto al oeste.

Método del paralelogramo

1. Elija una escala y determine la longitud de las flechas que corresponden a cada vector.

2. Dibuje a escala una flecha que represente la magnitud, sentido y dirección del primer vector.

3. Dibuje la flecha del segundo vector de modo que la cola de éste coincida con la cola del primer vector.

4. Trace desde la punta de la flecha del primer vector una recta paralela al segundo vector y desde la punta de la flecha del segundo vector una recta paralela al primer vector.

5. De esta manera se forma un paralelogramo. Dibuje el vector resultante con el origen (cola de los vectores) y la punta de flecha unida al vértice opuesto del paralelogramo.

6. Mida con regla y transportador para determinar la magnitud y dirección del vector resultante.

Ejemplo 1:

Encuentre la fuerza resultante sobre el burro de la figura 1.8, si el ángulo entre las dos cuerdas es de 120º. En un extremo se jala con una fuerza de 60 lb; y en el otro, con una fuerza de 20 lb.

Solución:

Utilizando una escala de 1cm = 10 lb se tiene que

60 lb = 6 cm 20 lb = 2 cm

En la figura 1.9 se construyó un paralelogramo, dibujando a escala las dos fuerzas a partir de un origen común y con

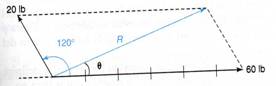Fig. 1.8 ¿Cuál es la fuerza resultante? El ángulo de 120º entre ellas. Al completar el paralelogramo se puede dibujar la resultante como una diagonal desde el origen. Al medir R y θ con una regla y un transportador se obtienen 52.9 lb para la magnitud y 19.1º para la dirección. Por consiguiente, R = 52.9 lb, 19.1º.

Fig. 1.9 Método el paralelogramo.

Ejemplo 2:

Dadas las componentes rectangulares de un vector, encontrar el vector resultante por el método del paralelogramo. Encuentre también el ángulo que forma la resultante con respecto al eje horizontal.

Solución:

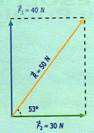Para encontrar la resultante basta con trazar primero las componentes F₁ y F₂ utilizando una escala conveniente y después, una paralela a F₁, a partir de F₂ y una paralela a F₂ a partir de F₁. La resultante será la línea que une al origen de los dos vectores con el punto donde hacen intersección las dos paralelas. Medimos la longitud de la resultante y vemos que aproximadamente mide 5 cm, éstos equivalen a 50 N y el ángulo de la resultante a 53º.

Ejercicio para clase:

1.- Encontrar por el método del paralelogramo la resultante, así como el ángulo que forma con el eje horizontal en cada una de las siguientes sumas de vectores.

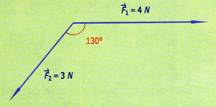
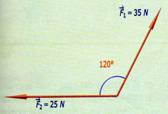
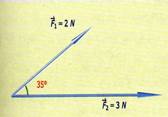a) b) c)

Ejercicios de tarea:

1.- Determine por el método del paralelogramo la fuerza F₂ y el ángulo correspondiente para que la lancha de la figura 1.10 se mueva hacia el este con una fuerza resultante de 650 N.

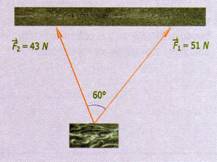2.- Determine el peso de un cuerpo que esta suspendido y sostenido por dos cuerdas, como se ve en la figura 1.11.

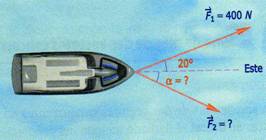
Fig. 1.10 Fig. 1.11

1.1.3 Componentes de los vectores y suma de vectores (Métodos analíticos).

La componente de un vector se define como su valor efectivo en una dirección dada. Un vector en dos dimensiones se puede resolver en dos vectores componentes que actúan a lo largo de dos dimensiones mutuamente perpendiculares. En general, podemos escribir las componentes x y y de un vector en términos de su magnitud F y su dirección θ.

F_x = F cos θ

F_y = F sen θ

donde θ es el ángulo entre el vector y el eje x, medido en dirección contraria a las manecillas del reloj. El signo de una componente dada se determina a partir del siguiente diagrama de vectores (Fig. 1.12).

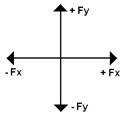
Fig. 1.12

Ejemplo 1:

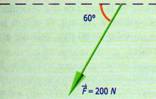
Encontrar las componentes rectangulares o perpendiculares del siguiente vector.

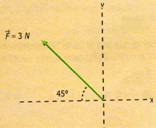Solución:

Escala 1 cm = 1 N

F_x = - F cos 45º = - (3N) (0.7071) = - 2.1213

F_y = F sen 45º = (3N) (0.7071) = 2.1213

Ejemplo 2:

Encuentre las componentes x y y de una fuerza de 400 N a un ángulo de 220° a partir del eje positivo, como muestra la figura 1.13.

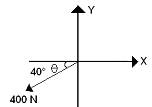
Solución:

θ = 220º - 180º = 40º

F_x = F cos θ = - 400 cos 40 = - (400 N) (0.776) = - 306.417 N

F_y = - F sen θ = - 400 sen 40 = - (400 N) (0.643) = - 257.115

Fig. 1.13

Ejercicio en clase:

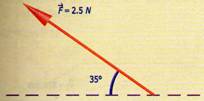
Encontrar las componentes rectangulares de los siguientes vectores.

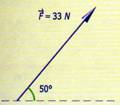
Ejercicios de tarea:

1.- Mediante una cuerda un niño jala un carro con una fuerza de 80 N, la cual forma un ángulo de 40º con el eje horizontal como se ve en la figura 1.14. Calcular:

a) El valor de la fuerza que jala el carro horizontalmente.

El valor de la fuerza que tiende a levantar el carro.

2.- Con ayuda de una cuerda se jala un bote aplicando una fuerza de 400 N, la cual forma un ángulo de 30º con el eje horizontal, como se ve en la figura 1.15. Calcular:

a) Determinar con el método analítico el valor de la fuerza que jala a la lancha horizontalmente.

b) Calcula el valor de la fuerza que tiende a levantar la lancha.

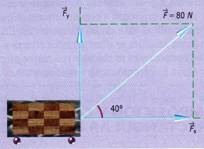
Fig. 1.14 Fig. 1.15

Método analítico para la suma de vectores aplicando la ley de los senos y la ley de los cosenos.

1. Para calcular la resultante entre dos vectores F₁ y F₂ debemos encontrar uno de los tres lados de un triángulo oblicuo, cuyos lados conocidos son F₁ y F_2. .

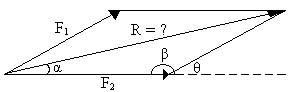
2. Aplicamos la ley de los cosenos, tomando en cuenta que en el triangulo oblicuo el ángulo formado por los dos vectores es β.

3. Para calcular el ángulo α que forma la resultante con respecto a la horizontal, aplicamos la ley de los senos:

Ejemplo 1:

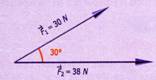Por el método de la ley de los senos y cosenos hallar la resultante y el ángulo que forma con la horizontal en la siguiente suma de vectores.

Solución:

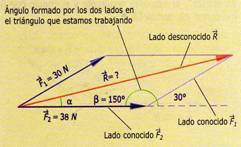
Primero debemos encontrar los tres lados de un triángulo oblicuo cuyos lados conocidos son los dos vectores. Aplicamos la ley de los cosenos, tomando en cuenta que en el triangulo oblicuo el ángulo formado por los dos vectores es de 150º.

R = 65.715

Para calcular el ángulo α que forma la resultante con respecto a la horizontal, aplicando la ley de los senos.

Ejemplo 2:

En la siguiente suma de vectores encontrar la resultante y el ángulo que forma con respecto al eje horizontal.

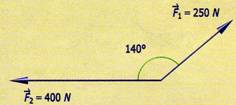
Solución:

R = 263.25

Ejercicios en clase:

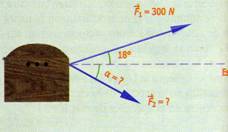
1.- Dos personas jalan mediante una cuerda cada una, un baúl de madera, como se ve en la figura 1.16. Una de las personas aplica una fuerza F₁ de 300N con un ángulo de 18º respecto al este. Determinar la fuerza F₂ que debe aplicar la otra persona y el ángulo que debe formar respecto al este para que el baúl se desplace hacia el este con una fuerza resultante de 450 N.

Fig. 1.16

2.- Encuentre el peso de un cuerpo que se encuentra suspendido del techo por dos cuerdas, las cuales ejercen una fuerza de 320 N y 400 N, y forman un ángulo de 80º.

Ejercicios de tarea:

1.- Mediante dos cables enganchados en la proa, un barco es remolcado por dos lanchas de motor. Una lleva una velocidad de 18 m/s al sur y la otra una velocidad de 15 m/s con dirección sureste, formando un ángulo de 60º respecto al sur. Encontrar la velocidad resultante del barco y el ángulo que forma respecto al sur.

2.- Una lancha de motor lleva una velocidad de 16 m/s al cruzar perpendicularmente hacia el norte la corriente de un río cuya velocidad es de 4 m/s al este. Determina la velocidad resultante que lleva la lancha y el ángulo formado respecto a la corriente del río.

Método de componentes para sumar vectores.

1. Dibuje cada vector a partir del cruce de los ejes imaginarios x y y.

2. Encuentre las componentes x y y de cada vector.

3. Halle la componente x de la resultante, sumando las componentes x de todos los vectores. (Las componentes a la derecha son positivas, y las que están a la izquierda con negativas).

R_x = ∑F_x = F1_x + F2_x + . . . + Fn_x

4. Encuentre las componentes y de la resultante sumando las componentes y de todos los vectores. (las componentes hacia arriba son positivas y las que van hacia abajo negativas.)

R_y = ∑F_y = F1_y + F2_y + . . . + Fn_y

5. Determine la magnitud, dirección y sentido de la resultante a partir de sus componentes perpendiculares.

Ejemplo 1:

Tres sogas están atadas a una estaca, y sobre ella actúan tres fuerzas: A = 20 lb, E; B = 30 lb, 30º NO; y C = 40 lb, 52º SO. Determine la fuerza resultante.

Solución:

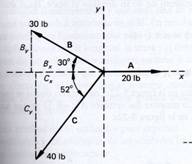Dibuje una figura representativa de cada fuerza. Se deben tener presentes dos cosas en la figura: a) todos los ángulos quedan determinados por el eje x, y b) las componentes de cada vector se indican como opuestas y adyacentes a los ángulos conocidos.

Encuentre las componentes x y y para cada vector. Note que la fuerza A no tiene componente en y. Se debe tener cuidado para asignar el signo correcto a cada componente. Por ejemplo B_x, C_x y C_y son negativas.

Sume las componentes x para obtener R_x.

R_x = Σ Fx = A_x + B_x + C_x = 20 – 30 cos 30º - 40 cos 52º = 20 lb – 26 lb – 24.6 lb = - 30.6 lb.

Sume las componentes y para obtener Ry.

R_y = Σ Fy = A_y + B_y + C_y = 0 + 30 sen 30º - 40 sen 52º = 15 – 31.5 = -16.5 lb

Ahora encuentre R y θ a partir de R_x y R_y.

θ = tan^-1 (0.539) = 28.3º SO (o 208.3º)

Ejemplo 2:

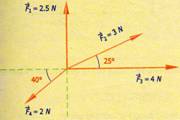Encontrar la resultante de la siguiente suma de vectores. Determinar también el ángulo que forma la resultante con respecto al eje horizontal.

Solución:

Σ Fx = F_1x + F_2x + F_3x + F_4x = 0 + 3 cos 25 + 4 – 2 cos 40 = 2.7189 + 4 – 1.532 = 5.1869 N

Σ F_y = F_1y + F_2y + F_3y + F_4y = 2.5 + 3 sen 25 + 0 – 2 sen 40 = 2.5 + 1.2678 – 1.2856 = 2.4822 N

θ = tan ^-1 ( 0.4785) = 25.6º = 25º36´

Ejercicios en clase:

1.- Calcula la fuerza resultante y su ángulo que actúa sobre el perno de la figura 1.17.

2.- Dos fuerzas actúan sobre el automóvil ilustrado en la fig. 1.18. La fuerza A es igual a 120 N, hacia el oeste, y la fuerza B e igual a 200 N a 60º NO. ¿Cuáles son la magnitud y la dirección de la fuerza resultante sobre el automóvil?

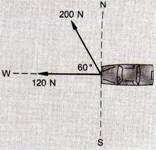
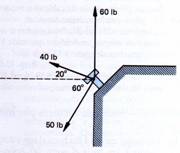
Fig. 1.17 Fig. 1.18

Ejercicios de tarea:

1.- Encontrar la resultante de las fuerzas concurrentes de la fig. 1.19 , así como el ángulo que forma respecto al eje x positivo.

2.- Encuentre las componentes rectangulares, la resultante de las velocidades de la fig. 1.20 y el ángulo que forma respecto al eje x positivo.

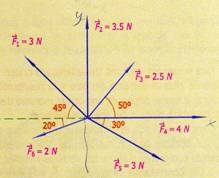3.- Hallar la resultante de la suma de los vectores de la fig. 1.21. Determinar también el ángulo formado respecto al eje x positivo.

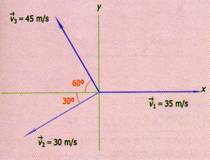
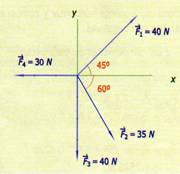
Fig. 1.19 Fig. 1.20 Fig. 1.21

1.1.4 Producto entre vectores.

Producto de un vector por un escalar.

El producto de un escalar k y de un vector se escribe: k y se define como un nuevo vector cuya magnitud es k veces mayor que la magnitud de . El nuevo vector tiene el mismo sentido que si k es positivo, sin embargo, si k es negativo, el vector resultante cambiará su magnitud y su sentido, o sólo su sentido en el caso que k sea igual a -1. Ejemplos:

Si = 5 N y k = 6 k = 6 x 5 N = 30 N

Si = 4 N y k = -1 k = -1 x 4 N = -4 N.

Producto escalar de dos vectores.

El producto escalar de dos vectores, llamado también producto punto, da como resultado una magnitud escalar. Por definición, el producto escalar de dos vectores es igual a multiplicar la magnitud de un vector por la componente perpendicular del otro vector, en la dirección del primero: = a b cos θ.

Producto vectorial de dos vectores.

El producto vectorial de dos vectores, llamado también producto cruz, da como resultado otro vector que siempre es perpendicular al plano formado por los dos vectores multiplicados: . Por definición, el producto vectorial de dos vectores es igual a multiplicar la magnitud de un vector por la componente perpendicular del otro vector con respecto al primero: = a b sen θ. Esta expresión representa únicamente la magnitud del vector , de manera que si se desea conocer su sentido se debe usar la regla de la mano derecha. La dirección siempre es perpendicular al plano formado por los vectores multiplicados.

1.2 Equilibrio de una partícula.

1.2.1 Introducción.

Las fuerzas pueden actuar de tal forma que causen el movimiento o lo eviten. Los grandes puentes deben diseñarse de modo que el esfuerzo global de las fuerzas evite el movimiento. Las armaduras, vigas, y cables, en conjunto, deben estar en equilibrio. Es decir, las fuerzas resultantes que actúan en cualquier punto de la estructura, deben estar equilibradas.

Cuando un cuerpo se encuentra en movimiento puede estar desplazándose de un punto a otro, girando sobre su propio eje, o bien, realizando ambos movimientos. Por ejemplo, cuando vemos pasar un autobús, los pasajeros efectúan un movimiento de traslación, pero las ruedas efectúan un movimiento de rotación y de traslación. En general, cualquier movimiento por complejo que sea puede ser reducido para su estudio a los dos tipos de movimiento señalados: traslación o de rotación.

1.2.2 Fuerza.

Siempre que interviene una fuerza, existe como mínimo una interacción entre dos cuerpos. Las fuerzas de contacto se producen cuando existe un contacto físico entre el cuerpo que ejerce la fuerza y el que la recibe. Cuando dos cuerpos interaccionan sin que exista contacto entre ellos, se presentan las llamadas fuerzas de acción a distancia. El efecto que una fuerza produce sobre un cuerpo depende de su magnitud, dirección y sentido, por tal motivo la fuerza es una magnitud vectorial. La unidad de fuerza en el sistema internacional es el newton (N) y en CGS es la dina.

El peso de un objeto (F_w) es la fuerza con que la gravedad tira al cuerpo hacia abajo. F_w = mg.

La tensión de una cuerda (F_T) es la fuerza con la que la cuerda tira del objeto al cual está unida.

Fuerza de fricción (F_f) es una fuerza tangencial sobre una superficie que se opone al deslizamiento de un objeto a través de una superficie adyacente con la que está en contacto. La fuerza de fricción es paralela a la superficie y opuesta, en sentido a su movimiento.

La fuerza normal (F_N) sobre una superficie que descansa (o se desliza) sobre una segunda superficie, es la componente perpendicular de la fuerza ejercida por la superficie de soporte sobre la superficie que se está siendo soportada.

1.2.3 Primera condición de equilibrio.

Para que un cuerpo este en equilibrio de traslación, la resultante de todas las fuerzas que actúan sobre él deben ser cero: = 0, o sea ∑Fx = 0 y ∑Fy = 0.

Ejemplo 1:

Dos niños sostienen una piñata cuyo peso es de 196 N, formando un ángulo de 140º con ambas cuerdas, como se ve en la figura 1.22. Calcular la fuerza aplicada por cada niño.

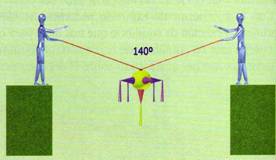
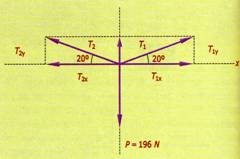
Fig. 1.22 Fig. 1.23 Diagrama de cuerpo libre

Solución:

El primer paso es dibujar el diagrama de cuerpo libre indicando las fuerzas que actúan sobre la piñata. Como el cuerpo esta en equilibrio, entonces: Σ Fx = 0 y Σ Fy = 0. Así podemos obtener el valor de las dos tensiones.

Σ Fx = 0 = T_1x – T_2x

Σ Fy = 0 = T_1y + T_2y – w

Σ Fx = T₁ cos 20 – T₂ cos 20 = 0

T₁ cos 20 = T₂ cos 20

T₁ = T₂

Σ Fy = T₁ sen 20 + T₂ sen 20 – 196 = 0

T₁ sen 20 + T₂ sen 20 = 196

Como T₁ = T₂ = T

2 T sen 20 = 196

Donde la fuerza aplicada por cada niño es de 286.54 N.

Ejemplo 2:

Determine los valores de las tensiones mostradas en la figura 1.24, si el objeto soportado pesa 600N.

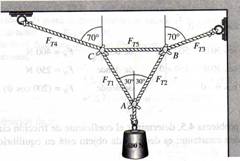
Solución:

Se escoge el nudo A como el objeto ya que se conoce una de las fuerzas que actúan sobre él. El peso actúa sobre el objeto verticalmente hacia abajo con un fuerza de 600 N de modo que el diagrama de cuerpo libre para el nudo es como se muestra en la figura 1.25. Al aplicar la primera condición de equilibrio para este diagrama de cuerpo libre obtenemos:

Σ Fx = 0 o F_T2 cos 60º - F_T1 cos 60 = 0

Fig. 1.24 Σ Fy = 0 o F_T1 sen 60 + F_T2 sen 60 – 600 = 0

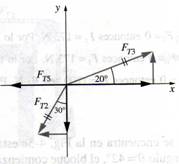
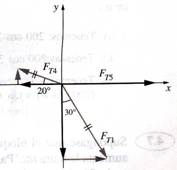
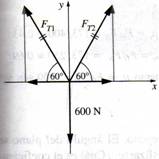
Fig. 1.25 Fig. 1.26 Fig. 1.27

F_T2 cos 60º = F_T1 cos 60

F_T2 = F_T1 = F_T

F_T sen 60 + F_T sen 60 = 600

2 F_T sen 60 = 600

Aislemos ahora el nudo B como objeto de estudio. El diagrama de cuerpo libre correspondiente se muestra en la figura 1.26. Sabemos que F_T2 = 346 N, y en consecuencia, las ecuaciones de equilibrio son:

Σ Fx = 0 o F_T3 cos 20º - F_T5 – 346 sen 30º = 0 651 N

Σ Fy = 0 o F_T3 sen 20º - 346 cos 30º = 0

F_T3 sen 20º = 346 cos 30º

877 cos 20º– 346 sen 30º = F_T5

F_T5 = 651 N

Por simetría F_T4 = F_T3 = 877 N

Ejercicios en clase:

1.- Hallar las tensiones T₁, T₂ y T₃ del sistema mostrado en la figura 1.28.

2.- Encuentre la tensión en las cuerdas A y B de la figura 1.29.

3.- La figura 1.30 muestra una persona de 800 N colgada en el centro de una cuerda. Calcula las tensiones T₁ y T₂ en ambas partes de la cuerda.

4.- La figura 1.31 muestra la forma caprichosa en que una araña a tejido su tela. Si la araña pesa 3x10^-2 N, determina la tensión de cada una de las partes de la tela.

5.- Un cuerpo cuyo peso es de 500 N está suspendido de una armadura, como se ve en la figura 1.32. Determinar el valor de la tensión de la cuerda y el empuje de la barra.

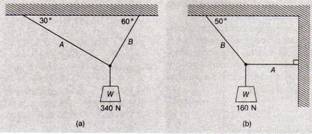
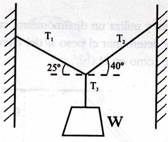
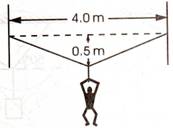
Fig. 1.28 Fig. 1.29 Fig. 1.30

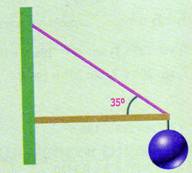
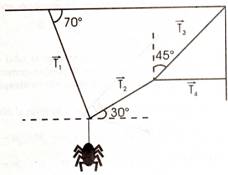
Fig. 1.31 Fig. 1.32

Ejercicios de tarea:

1.- Tres ladrillos idénticos están atados entre sí por medio de cuerdas y penden de una balanza que marca en total 24 N. ¿Cuál es la tensión de la cuerda que soporta el ladrillo inferior?¿Cuál es la tensión en la cuerda que se encuentra entre el ladrillo de en medio y el ladrillo superior?

2.- Calcule la tensión en la cuerda A y la compresión B en la figura 1.33.

3.- En la figura 1.34 las poleas no presentan fuerza de fricción y el sistema cuelga en equilibrio. Si el peso de F_W3 es de 200 N. ¿Cuáles son los valores de F_W1 y F_W2?

4.- En la figura 1.35 las cuerdas pueden soportar una tensión máxima de 80N. ¿Cuál es el máximo valor de F_w que pueden soportar las cuerdas?

5.- Suponga que el peso y el rozamiento de las poleas que se muestran en la fig. 1.36 son despreciables. ¿Cuál es el valor de F_w para que el sistema permanezca en equilibrio?

6.- Un cuerpo de 490 N se encuentra suspendido del techo por medio de dos cuerdas como se ve en la fig. 1.37. Determine la tensión en cada una de ellas.

7.- Encuentre la tensión en las cuerdas A y B de la fig. 1.38 (a) y (b).

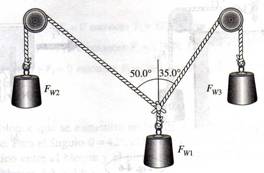
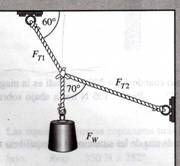
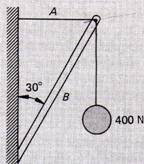
Fig. 1.33 Fig. 1.34 Fig. 1.35

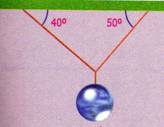
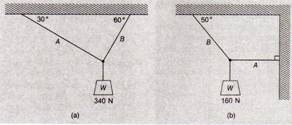
Fig. 1.36 Fig. 1.37 Fig. 1.38

Ejemplo 3:

Un bloque de 200 lb descansa sobre un plano inclinado sin fricción, que tiene una pendiente de 30º. El bloque esta atado a una cuerda que pasa sobre una polea sin fricción colocada en el extremo superior del plano y va atada a un segundo bloque. ¿Cuál es el peso del segundo bloque si el sistema se encuentra en equilibrio?(Ignore el peso de la cuerda).

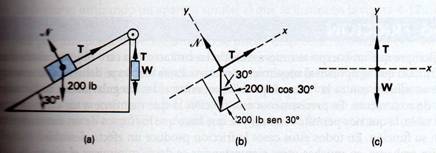Fig. 1.39

Solución:

Después de hacer un bosquejo que describa la situación, se construye un diagrama de cuerpo libre para cada cuerpo como se observa en la figura 1.39. Al aplicar la primera condición de equilibrio para el segundo bloque (Fig. 1.39c), encontramos que:

Σ Fy = T – w = 0

T = w

Puesto que la cuerda es continua y el sistema no está afectado por la fricción, la tensión de la figura 1.39b para el bloque de 200 lb también debe ser igual al peso w. Considerando el diagrama para el bloque de 200 lb, determinamos las componentes de cada fuerza en la manera siguiente:

Σ Fx = T – 200 sen 30º = 0

T = 200 sen 30º = 100 lb

Por lo tanto w = 100 lb, puesto que T = w. Por consiguiente se requiere un peso de 100 lb para conservar el equilibrio.

Ejemplo 4:

Una caja de 50N se desliza sobre el piso con una velocidad constante por medio de una fuerza de 25 N, como se muestra en la figura 1.40. a) ¿Cuál es el valor de la fuerza de fricción que se opone al movimiento? b) ¿Cuál es el valor de la fuerza normal? c) Determine μ_c entre la caja y el piso.

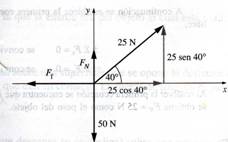
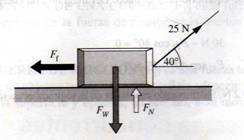Fig.1.40 Fig. 1.41

Solución:

En la figura 1.40 la fuerza de fricción es F_f y la fuerza normal , la fuerza de soporte ejercida por el piso, es F_N. El diagrama de cuerpo libre y las componentes de las fuerzas se muestran un la figura 1.41. Ya que la caja se mueve con velocidad constante, se encuentra en equilibrio. La primera condición de equilibrio nos dice que:

∑ Fx = 0 o 25 cos 40° - F_f = 0

Entonces encontramos el valor de F_f.

F_f = 25 cos 40° = 19.2 N

Para determinar la fuerza normal usamos la ∑ Fy,

∑ Fy = 0 o F_N + 25 sen 40° - 50 = 0

F_N = 50 - 25 sen 40° = 33.9 N

Para obtener μ_c tenemos:

μ_c = F_f / F_N = 19.2 / 33.9 = 0.57

Ejercicios en clase:

1.- Los objetos de la figura 1.42 están en equilibrio. Determine el valor de la fuerza normal en cada caso.

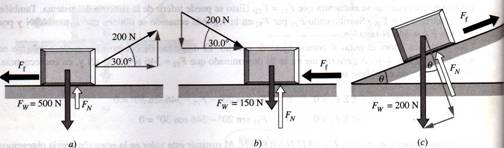
Fig. 1.42

2.- Jalado por un bloque de 8N como se muestra en la figura 1.43, un bloque de 20N se desliza hacia la derecha con velocidad constante. Calcular el μ_c entre el bloque y la mesa. Supóngase que la fricción en la polea es despreciable.

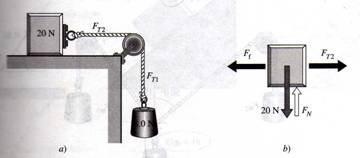
Fig. 1.43

3.- Si en la figura 1.44 la fricción entre el bloque y el plano inclinado es despreciable, ¿Cuál debe ser el peso F_w si se quiere que el bloque de 200 N permanezca en reposo?

4.- El sistema que se muestra en la figura 1.44 permanece en reposo cuando F_w = 220 N. ¿Cuál es la magnitud y la dirección de la fuerza de fricción sobre el bloque de 200 N?

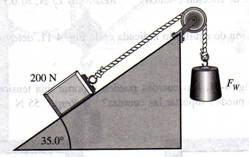Fig. 1.44

Ejercicios de tarea:

1.- Encuentra la fuerza normal que actúa sobre el bloque en cada una de las situaciones de equilibrio mostradas en la figura 1.45.

2.- El sistema de la figura 1.46 se encuentra próximo al límite de deslizamiento. Si F_w = 8 N, ¿cuál es el valor del coeficiente de fricción estático entre el bloque y la mesa?

3.- ¿Qué fuerza T, a un ángulo de 30° por encima de la horizontal, se requiere para arrastrar un bloque de 40 lb hacia la derecha a velocidad constante, si μ_k = 0.2? Figura 1.47

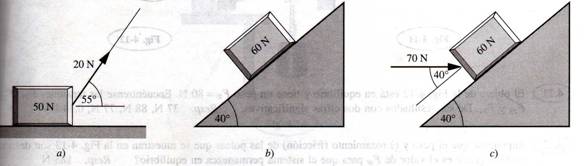
Fig. 1.45

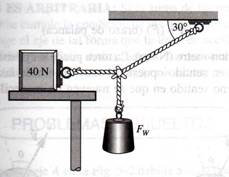
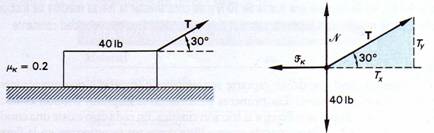Fig. 1.46 Fig. 1.47

4.- Un bloque de 100 N está en reposo en un plano inclinado a 30°. Si μ_k = 0.1, ¿Qué fuerza P paralela al plano y dirigida hacia arriba del plano hará que el bloque se mueva (a) hacia arriba con velocidad constante y (b) hacia abajo del plano inclinado con velocidad constante? Figura 1.48

5.- ¿Cuál es el ángulo máximo θ de la pendiente de un plano inclinado que permite que un bloque de peso W no se deslice hacia abajo a lo largo del plano? Figura 1.49

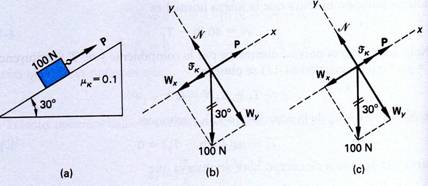Fig. 1.48

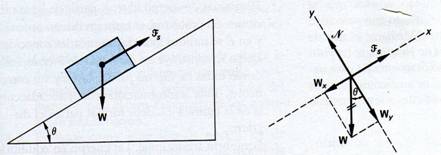Fig. 1.49

1.2.4 Tercera Ley de Newton.

La tercera ley de Newton o ley de las interacciones, se enuncia en los siguientes términos: Cuando un cuerpo A ejerce una fuerza sobre un cuerpo B, éste reacciona sobre A ejerciendo una fuerza de la misma intensidad y dirección pero diferente sentido.

1.2.5 Equilibrio de una partícula, la segunda condición de equilibrio.

Para que un cuerpo este en equilibrio de rotación, la suma de los momentos o torcas de las fuerzas que actúan sobre él respecto a cualquier punto debe ser igual a cero. ∑ M = 0.

Ejemplo 1:

Considere la situación que se presenta en la figura 1.50. Una viga uniforme que pesa 200 N está sostenida por dos soportes A y B. De acuerdo con las distancias y fuerzas que aparecen en la figura, ¿cuáles son las fuerzas ejercidas por los soportes?

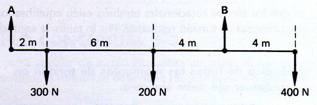
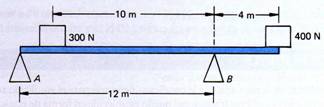
Fig. 1.50 Bosquejo del sistema. Fig. 1.51 Diagrama de cuerpo libre.

Solución:

Se traza un diagrama de cuerpo libre para que muestre claramente todas las fuerzas y las distancias entre ellas ( figura 1.51) . Nota que se considera que todo el peso de la viga uniforme actúa en su centro. En seguida aplicamos la primera condición de equilibrio, Σ Fy = 0.

Σ Fy = A + B – 300N – 200N – 400N = 0

A + B = 900N

Puesto que esta ecuación tiene dos incógnitas, es preciso tener más información. Por lo tanto aplicamos la segunda condición de equilibrio. En primer lugar, debemos seleccionar un eje desde el cual podamos medir brazos de palanca. La elección lógica es el punto de aplicación de alguna fuerza desconocida. Eligiendo el eje en B, el brazo de palanca en esta fuerza es cero. La suma de los momentos de torsión respecto a B dan por resultado la siguiente ecuación:

Σ M = - A(12m) + (300N)(10m) + (200N)(4m) – (400N)(4 m) = 0

Note que la fuerza de 400N y la fuerza A tienden a producir una rotación en el sentido de las manecillas del reloj con respecto a B. (Sus momentos de torsión fueron negativos). Simplificando se obtiene:

- (12m)A + 3000 N.m – 1600 N.m + 800 N.m = 0

- (12m) A = - 2200 N.m

A = 183.33 N

Ahora para determinar la feurza ejercida por el soporte B, tomemos en cuenta de nuevo la ecuación obtenida a partir de la primera condición de equilibrio:

A + B = 900 N

B = 900N – 183.33 N

B = 716.66 N

Como comprobación de este resultado, podemos elegir el eje de rotación en A y luego aplicar la segunda condición de equilibrio para determinar B.

Ejemplo 2:

Una escalera se recarga contra una pared lisa, como se muestra en la figura 1.52. La escalera pesa 200N y su centro de gravedad está a 0.4 L medido desde el pie y a lo largo de la escalera, L es la longitud de la escalera. A) ¿Cuál debe ser la magnitud de la fuerza de fricción al pie de la escalera para que ésta no resbale? B) ¿Cuál es el coeficiente de fricción estático?

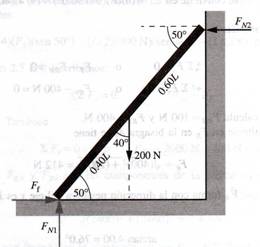Fig. 1.52

Solución:

Se desea encontrar la fuerza de fricción F_f. Note que no existe fuerza de fricción entre la escalera y la pared. Haciendo suma de momentos en la base de la escalera (punto A).

∑ M_A = - (0.40 L) (200 sen 40°) + L (F_N2 sen 50° ) = 0

F_N2 = 67.1 N

Aplicando la primera condición de equilibrio.

∑Fx = F_f – F_N2 = 0

F_f = 67.1 N

∑Fy = F_N1 - 200 = 0

F_N1 = 200 N

μ_e = F_f / F_N1 = 0.34

1.2.6 Centros de masa.

El centro de masa de un cuerpo se localiza en aquel punto en el cual para cualquier plano que pasa por él los momentos de las masas a un lado del plano son iguales a los momentos de las masas del otro lado.